미래연구소 http://futurelab.creatorlink.net/
미래연구소
AI, 인공지능 Deep Learning beginner 미래연구소 딥러닝 입문 스터디 / 모집인원 : 25명 (선착순 마감) 수강료 : 월 15만원 / (Coursera 강의 수강료 월 5만원 개인결제)
futurelab.creatorlink.net
Vectorizing Logistic Regression (forward propagation)
m개의 training sample이 있을 때 첫번째 training sample을 예측하려면
$z^{(1)}=w^{(T)}x^{(1)}+b$
$a^{(1)}=\sigma(z^{(1)})$
이 식들을 계산해야 한다.
두번째 training sample을 예측하려면
$z^{(2)}=w^{(T)}x^{(2)}+b$
$a^{(2)}=\sigma(z^{(2)})$
을 계산해야 한다.
training sample이 m개가 있다면 위의 식을 m번 계산해야 한다.
이 과정들을 for문 없이 계산하는 방법이 있다.
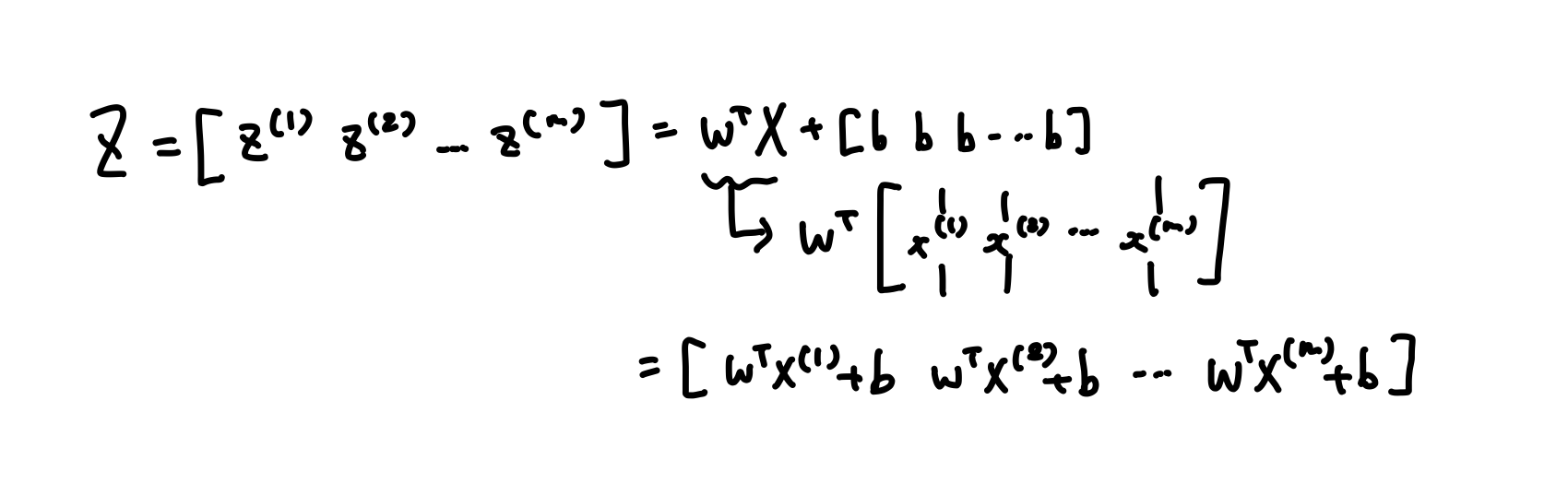
이 식을 numpy로 나타내는 함수는
$Z=np.dot(w^{(T)}, X)+b$이다.
※여기서 b는 (1, 1) 행렬이라고 할 수 있는 실수이다.
위 vector와 이 실수를 더하면 파이썬은 실수 b를 자동으로 (1, m)행 vector ($\begin{bmatrix} b & b & \cdots & b \end{bmatrix}$)로 바꿔준다.
이 연산을 파이썬에서 “broadcasting”이라고 부른다.
다음으로 계산하고 싶은 것은 $a^{(1)} \cdots a^{(m)}$을 한 번에 계산하는 것이다.
앞의 식에서 그랬던 것처럼 $a^{(i)}$를 한 줄로 적어
$A = \begin{bmatrix} a^{(1)} & a^{(2)} & \cdots & a^{(m)} \end{bmatrix}$로 새롭게 정의한다.
저번 주차에서 공부한 sigmoid 함수를 구현하여 이 함수가 위에서 구한 Z를 입력으로 받고 효율적으로 A를 반환한다.
→ $A = \sigma(Z)$
정리하면, 이제 vectorization을 통해 z와 a를 하나씩 계산하기 위해 m개의 training sample을 반복하는 대신 한 줄의 코드($Z=np.dot(w^{(T)}, X)+b$)로 모든 z를 동시에 계산하고, 적절한 sigmoid 함수의 구현으로 한 줄의 코드로 모든 a를 동시에 계산할 수 있다.
Vectorizing Logistic Regression (backward propagation)
Gradient Descent를 계산하기 위해 우선 첫 sample인 $\operatorname{d}\!{z}^{(1)}=a^{(1)}-y^{(1)}$을 계산한다.
그 다음 샘플들도 계산한다. $\operatorname{d}\!{z}^{(2)}=a^{(2)}-y^{(2)}, \cdots ,\operatorname{d}\!{z}^{(m)}=a^{(m)}-y^{(m)}$
이제 정의할 것은 $\operatorname{d}\!Z$이다.
$\operatorname{d}\!Z = \begin{bmatrix} \operatorname{d}\!{z}^{(1)} & \operatorname{d}\!{z}^{(2)} & \cdots & \operatorname{d}\!{z}^{(m)} \end{bmatrix}$
이것은 $\operatorname{d}\!{z}^{(1)}, \operatorname{d}\!{z}^{(2)}$ 부터 $\operatorname{d}\!{z}^{(m)}$까지 모든 $\operatorname{d}\!z$를 가로로 쌓은 것이며, (1,m) 행렬 혹은 m차원 row vector가 이다.
$A=\begin{bmatrix} a^{(1)} \cdots a^{(m)} \end{bmatrix}, Y= \begin{bmatrix} y^{(1)} \cdots y^{(m)} \end{bmatrix}$일 때
$dZ=A-Y=\begin{bmatrix} a^{(1)}-y^{(1)} & a^{(2)}-y^{(2)} & \cdots & a^{(m)}-y^{(m)} \end{bmatrix}$로 계산될 수 있다는 걸 알 수 있다.
첫 요소인 $a^{(1)}-y^{(1)}$은 $\operatorname{d}\!{z}^{(1)}$의 정의와 정확히 일치하고 나머지 요소도 정확히 일치한다.
따라서 $\operatorname{d}\!$Z 한 줄의 코드로 모든 것을 동시에 계산할 수 있다.
위에서 배운 구현에서 이미 하나의 for문을 제거했지만 training sample을 계산하는 두 번째 for문은 여전히 남아있었다.
$\operatorname{d}\!w$를 0 vector로 초기화 해준 뒤, → $\operatorname{d}\!w=0$
training sample을 순환해줘야 했다.
$\operatorname{d}\!w += x^{(1)}\operatorname{d}\!z^{(1)}$
$\operatorname{d}\!w += x^{(2)}\operatorname{d}\!z^{(2)}$
$\vdots$
$\operatorname{d}\!w += x^{(m)}\operatorname{d}\!z^{(m)}$
와 같이 $\operatorname{d}\!w$에 m번을 반복해 추가해줘야 했다.
그 다음 $\operatorname{d}\!w$를 m으로 나눠줬다. -> $\operatorname{d}\!w /= m$
$\operatorname{d}\!b$도 위와 같은 과정을 거쳐야 했다.
$\operatorname{d}\!b=0$
$\operatorname{d}\!b += \operatorname{d}\!z^{(1)}$
$\operatorname{d}\!b += \operatorname{d}\!z^{(2)}$
$\vdots$
$\operatorname{d}\!b += \operatorname{d}\!z^{(m)}$
$\operatorname{d}\!b /= m$
위의 구현에서 이미 하나의 for문을 제거해서 이미 $\operatorname{d}\!w$는 vector이고 $\operatorname{d}\!z^{(1)}, \operatorname{d}\!z^{(2)}, \cdots \operatorname{d}\!z^{(m)}$ 은 따로 갱신하지 않았다.
하지만 m개의 training sample에 대한 for문이 남아있다.
이제 이 연산을 vectorization할 것이다.
$\operatorname{d}\!b$에 대한 vectorization 구현을 살펴보면 모든 $\operatorname{d}\!z$를 더하고 m으로 나눠주는 것이다.
$\operatorname{d}\!b$는 i가 1부터 m까지일 때 $\operatorname{d}\!z^{(i)}$의 합을 m으로 나눈 값이다.
→$\operatorname{d}\!b = \frac{1}{m}\sum_{i=1}^m \operatorname{d}\!z^{(i)}$
여기서 모든 $\operatorname{d}\!z$는 row vector이다.
numpy를 통해 구현할 때는 $ \frac{1}{m}np.sum(\operatorname{d}\!Z)$로,
단순히 $\operatorname{d}\!Z$를 가지고 np.sum 함수를 호출하면 $\operatorname{d}\!b$를 반환한다.
$\operatorname{d}\!W$는 다음과 같다.
$\operatorname{d}\!W=\frac{1}{m}X\operatorname{d}\!Z^{(T)}$
다음을 수식으로 정리하면 다음과 같다.
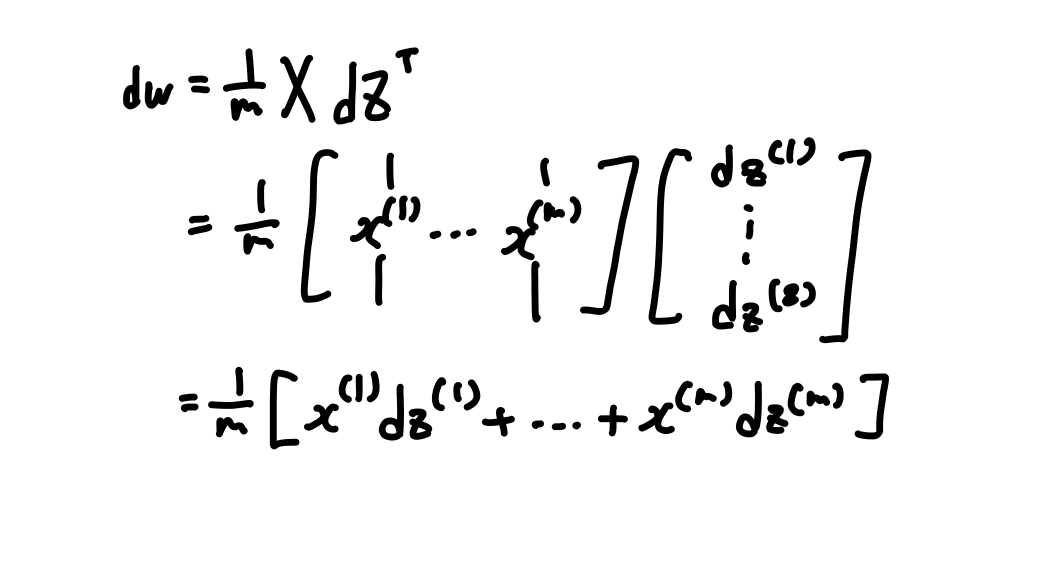
이제 $\operatorname{d}\!W$도 한 줄의 코드로 계산할 수 있다.
결론적으론 $\operatorname{d}\!b =\frac{1}{m}np.sum(\operatorname{d}\!Z)$로 $\operatorname{d}\!b$를 계산하고
$\operatorname{d}\!W=\frac{1}{m}X\operatorname{d}\!Z^{(T)}$로 $\operatorname{d}\!W$를 계산한다.
이제 for문 없이 이 값들을 계산할 수 있게 된다.
이제까지 다루었던 것을 모아 Logistic Regression을 어떻게 구현하는지 살펴보자.
아래의 식들은 기존의 vectorization을 하지 않은 비효율적인 구현이다.

이제까지는$\operatorname{d}\!w$를 for문으로 $\operatorname{d}\!w_1, \operatorname{d}\!w_2 \cdots \operatorname{d}\!w_m$를 하나하나 순환하는 대신 vector 값으로 바꿔서 모든 것이 vector 값인 $\operatorname{d}\!w += x^{(i)}\operatorname{d}\!z^{(i)}$로 대체했다.
이제는 이 for문 뿐만 아니라 위의 for문(for i = 1 to m;)도 제거할 수 있다는 것을 보겠다.
우리는 $Z=w^{(T)}X+b$라는 것을 알고 있고 이에 상응하는 코드는 $np.dot(w^{(T)},X)+b$이다.
그리고 $A=\sigma(Z)$
이 식들은 for문의 1, 2번 줄의 식의 모든 i에 대한 값들을 계산한 것이다.
앞의 내용에서 처럼 $\operatorname{d}\!Z=A-Y$이고 이 식은 for문의 4번 줄의 식의 모든 i에 대한 값을 계산한 것이다.
마지막으로 $\operatorname{d}\!w=\frac{1}{m}X\operatorname{d}\!Z^{(T)}$이고
$\operatorname{d}\!b = \frac{1}{m}np.sum(\operatorname{d}\!Z)$가 된다.
이제 Gradient Descent는 $w := w-\alpha\operatorname{d}\!w$가 되고,
$B := b-\alpha\operatorname{d}\!b$가 된다.
(‘=’ 왼쪽에 ‘:’을 붙인 것은 할당이라는 것을 명시해주는 것이다.)
이 식들을 정리하면 다음과 같다.

물론 가능한 한 for문을 줄여야 하지만 Gradient Descent을 여러 번 반복하고 싶다면 반복 횟수에 따라 for문이 필요하다.
Neural Network

Logistic regression에서는 z와 a를 한 번만 계산하고 Loss function을 계산했지만,
Neural Network(=NN)에서는 z와 a를 여러 번 계산해주고 Loss function을 계산해준다.
Logistic regression에서는 도함수 계산을 위해 backward propagation을 해줬다.
NN에서도 마찬가지로 backward propagation을 해준다.

입력 $x_1, x_2, x_3$이 세로로 쌓여 있는 층은 NN의 input layer라고 불린다.
다음 층은 hidden layer라고 불린다.
하나의 노드로 이루어진 마지막 층은 output layer라고 불리며, 예측 값인 $\hat {y}$의 계산을 책임진다.
hidden layer의 실제 값은 training set에 기록되어 있지 않다.
input값과 output값은 알 수 있지만 hidden layer의 값들은 알 수 없다.
따라서 hidden layer라는 이름은 training set에서 볼 수 없다는 걸 의미한다.
vectorization한 입력 값을 X라고 나타냈었는데, 입력 값의 다른 표기법은 $a^{[0]}$이다.
a는 활성 값을 의미하고 NN의 layer들이 다음 layer로 전달해주는 값을 의미한다.
input layer는 X를 hidden layer로 전달해준다.
따라서 $a^{[0]}$은 input layer의 활성 값이라고 부른다.
다음 층인 hidden layer는 활성 값 $a^{[1]}$을 만든다.
첫 번째 노드는 $a_1^{[1]}$을 만들고, 두 번째 노드는 $a_2^
{[1]}$을 만든다.
세,네 번째 노드는 각각 $a_3^{[1]}, a_4^{[1]}$을 만든다.
따라서 $a^{[1]}$은 4d array가 된다.
4d array인 이유는 이 hidden layer에 hidden unit이 4개 있기 때문이다.
다음으로 output layer는 실수 값 $a^{[2]}$를 만들게 된다.
따라서 $\hat{y}$은 $a^{[2]}$의 값을 가지게 된다.
Logistic regression에서 $\hat{y}$이 a의 값을 가지는 것과 비슷하다.
Logistic regression에선 output layer가 하나만 있어서 대괄호 위첨자를 쓰지 않았지만,
NN에서는 위첨자를 사용해 어떤 층에서 만들어진 건지 표기해준다.
이 NN는 “2 layer NN”라고 불리는데, 2 layer인 이유는 NN에서 layer를 셀 때 input layer는 세지 않기 때문이다.
따라서 hidden layer가 첫 번째 층이고 output layer가 두 번째 층이다.
Input layer를 0번째 layer라고 하기 때문에, 이 NN엔 input layer, hidden layer, output layer 이렇게 layer가 3개 있다고 할 수도 있다.
hidden layer는 매개 변수 $w^{[1]}$와 $b^{[1]}$에 관련되어 있고, 첫 번째 layer에 관련된 변수이기 때문에 위첨자 [1]을 붙인다.
w는 (4, 3) vector가 되고, b는 (4, 1) vector가 된다.
이때 w는 hidden 노드가 네 개 있고, input이 세 개 이기 때문에 (4, 3) vector가 된다.
output layer도 비슷하게 $w^{[2]}$와 $b^{[2]}$에 관련되어 있고, 각각 (1, 4) vector와 (1, 1) vector가 된다.
w는 output 노드 한 개가 있고, hidden 노드가 네 개이기 때문에 (1, 4) vector가 된다.
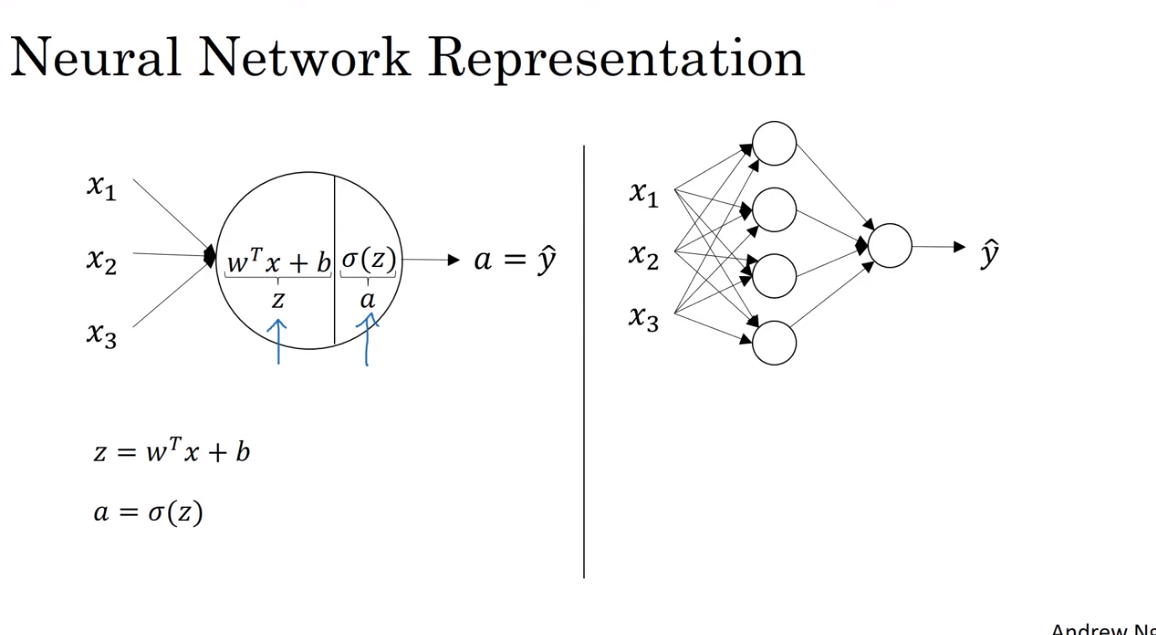
NN에서 hidden layer를 계산하는 과정이다.
우선, Logistic regression을 나타내는 왼쪽 그림은 두 단계의 계산을 나타낸다.
NN에선 hidden layer에 있는 노드 수만큼 이 과정을 반복한다.
이 계산들을 나타내면 다음과 같다.

위 식들을 for문으로 구현하면 안 좋다는 것을 알고 있기 때문에 vectorization한다.

output layer은 $a^{[1]}$을 x로 다시 두 단계의 계산을 한다.
$z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}$
$a^{[2]}=sigmoid(z^{[2]})$
이때, w는 (1, 4), a는 (4, 1), b는 (1, 1) vector이므로 $a^{[2]}$는 (1, 1)인 상수가 나오게 된다.
정리하면, 이 NN의 출력 값을 계산하는 데엔 다음의 코드 네 줄만 필요하다.
$z^{[1]}=W^{[1]}a^{[0]}+b^{[1]}$
$a^{[1]}=sigmoid(z^{[1]})$
$z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}$
$a^{[2]}=sigmoid(z^{[2]})$
'Computer Science > Deep Learning' 카테고리의 다른 글
| 미래연구소 딥러닝 4주 차 (Numpy 특강 3) (0) | 2020.08.02 |
|---|---|
| 미래연구소 딥러닝 4주 차 (0) | 2020.08.02 |
| 미래연구소 딥러닝 3주 차 ( Numpy 특강 2) (0) | 2020.07.25 |
| 미래연구소 딥러닝 2주 차 (0) | 2020.07.19 |
| 미래연구소 딥러닝 2주 차 예습 (0) | 2020.07.15 |
