미래연구소 http://futurelab.creatorlink.net/
미래연구소
AI, 인공지능 Deep Learning beginner 미래연구소 딥러닝 입문 스터디 / 모집인원 : 25명 (선착순 마감) 수강료 : 월 15만원 / (Coursera 강의 수강료 월 5만원 개인결제)
futurelab.creatorlink.net
Activation Function의 배경지식
activation의 미분계수가 0에 가까우면(=activation의 접선 기울기가 0에 가까우면) $\operatorname{d}\!W$가 감소하게 되고, Gradient Descent가 잘 일어나지 않는다. 즉, 학습이 일어나지 않는다. 이러한 Gradient Descent가 잘 일어나지 않는 현상(=gradient가 0에 가까워지는 현상)을 'vanishing gradient'라고 한다.
tanh function
지금까지는 hidden layer와 output layer에서 sigmoid 함수를 사용했다.
하지만 sigmoid 함수 말고 다른 함수가 더 좋을 수도 있다.
다음은 NN(Neural Network)의 출력 값을 계산하는 코드이다.
$z^{[1]}=W^{[1]}a^{[0]}+b^{[1]}$
$a^{[1]}=sigmoid(z^{[1]})$
$z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}$
$a^{[2]}=sigmoid(z^{[2]})$
그 중 빨간색으로 표시된 두 줄만 sigmoid 함수를 쓰는 단계이다.
여기서 sigmoid 함수 대신 다음과 같이 ‘g’로 표시된 함수를 사용할 수 있다.
$z^{[1]}=W^{[1]}a^{[0]}+b^{[1]}$
$a^{[1]}=$$g(z^{[1]})$
$z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}$
$a^{[2]}=$$g(z^{[2]})$
g는 sigmoid 함수가 아닌 non-linear 함수일 수 있다.
sigmoid 함수보다 대부분의 경우 좋은 것은 tanh 함수이다.

다음 그래프의 가로는 z축이며, 세로는 a축이다.
tanh 함수의 공식은
$a=tanh(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}$이다.
수학적으로 sigmoid 함수를 조금 옮긴 꼴이다.
sigmoid 함수와 비슷하지만 원점을 지나고 비율이 달라졌다.
또한 a의 값이 -1과 1 사이가 됐다.
hidden unit에 대해 g(z)를 tanh(z)로 놓는다면 거의 항상 sigmoid 함수보다 좋다.
learning algorithm을 훈련할 때 평균값의 중심을 0으로 할 때가 있다.
sigmoid 함수 대신 tanh 함수를 쓴다면
값이 -1에서 +1 사이이기 때문에 평균값이 0.5 대신 0에 더 가깝게 만드는 효과가 있다.
이렇게 해주면 다음 층의 학습을 더 쉽게 해 준다.
이러한 이유 때문에 sigmoid 함수보다 tanh 함수가 더 많이 쓰인다.
하지만 output layer는 예외이다.
y가 0이나 1이라면 $\hat{y}$은 -1과 1 사이 대신 0과 1 사이로 출력하는 게 더 좋기 때문이다.
정리하자면, hidden layer에선 tanh 함수를 쓰고 output layer에선 sigmoid 함수를 쓴다.
즉, 다른 layer에서는 다른 활성화 함수를 쓸 수 있는 것이다.
또한 다른 layer에서 다른 활성화 함수가 쓰였다는 것을 보여주기 위해 대괄호 위 첨자를 쓸 수 있다. → $g^{[1]}, g^{[2]}, \cdots$
sigmoid 함수와 tanh 함수의 단점은 z가 굉장히 크거나 작으면 함수의 도함수가 굉장히 작아진다는 것이다.
z가 크거나 작으면 함수의 기울기가 0에 가까워지고 Gradient Dscent가 느려질 수 있다.
ReLU function
머신러닝에서 인기 있는 함수는 ReLU 함수이다.
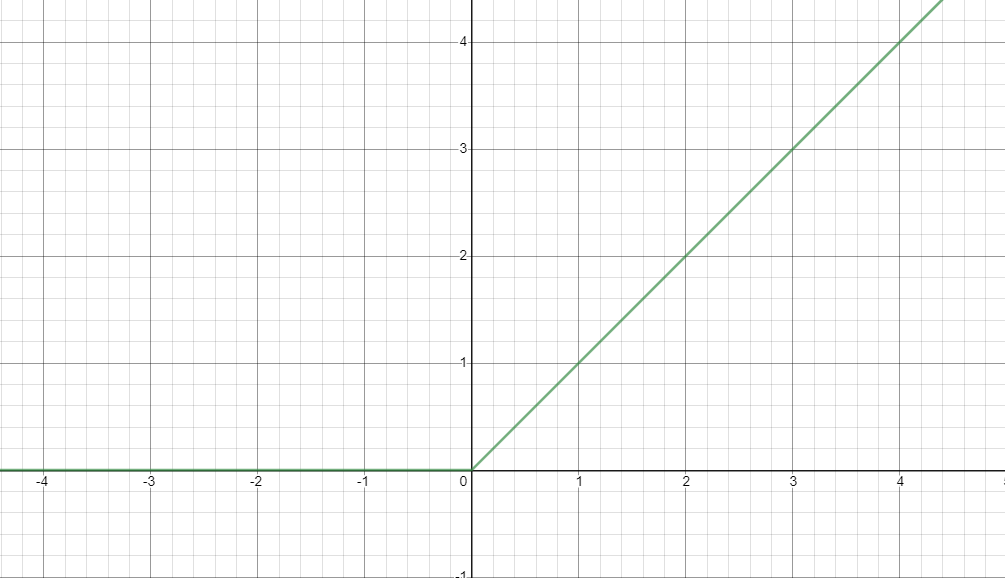
다음은 ReLU 함수의 형태이고, $a=max(0,z)$이다.
이 함수는 z가 양수일 때는 도함수가 1이고 z가 음수이면 도함수가 0이 된다.
엄밀히 따지면 z=0일 때의 도함수는 정의되지 않았지만 컴퓨터가 구현하면 z가 정확히 0이 될 확률은 굉장히 낮기 때문에 걱정하지 않아도 된다.
z가 0일 때 도함수가 1이나 0이라고 가정해도 잘 작동한다.
함수를 선택할 때는 우선, binary classification에서의 output layer에서는 자연스럽게 sigmoid 함수를 사용한다.
다른 경우에는 ReLU 함수가 기본값으로 많이 사용된다.
hidden layer에서 어떤 함수를 써야 할지 모르겠다면 그냥 ReLU 함수를 쓰는 것이 좋다.
요즘에는 ReLU 함수가 많이 쓰이지만 가끔 tanh 함수도 쓴다.
ReLU 함수의 단점 중 하나는 z가 음수일 때 도함수가 0이라는 것이다.
실제로는 잘 되긴 하지만 다른 버전인 Leaky ReLU 함수도 있다.
Leaky ReLU 함수는 z가 음수일 때 도함수가 0인 대신 약간의 기울기를 준다.
실제로는 많이 쓰이지 않지만 ReLU보다 좋은 결과를 보여준다.
아무거나 골라도 되지만 하나만 골라야 한다면 보통 ReLU 함수를 쓴다.
ReLU 함수와 Leaky ReLU 함수의 장점은 대부분의 z에 대해 기울기가 0과는 매우 다르다는 것이다.
따라서 sigmoid 함수나 tanh 함수 대신 ReLU 함수를 쓴다면 NN은 훨씬 더 빠르게 학습할 수 있다.
학습을 느리게 하는 원인인 함수의 기울기가 0에 가까워지는 것을 막아 주기 때문이다.
ReLU 함수는 z의 절반에 대해 기울기가 0이지만 실제로는 충분한 hidden unit의 z는 0보다 크기 때문에 실제로는 잘 동작한다.
각 함수의 장단점
1) sigmoid function
binary classification의 output layer라는 특수한 상황에 적합하다.
하지만 Gradient Descent의 속도 저하(vanishing gradient)를 일으키기 때문에, binary classification의 hidden layer 외에는 거의 쓰지 않는 것이 좋다.
2) tanh function
sigmoid보다는 vanishing gradient가 덜하다.
따라서 sigmoid 함수보다 tanh 함수가 더 성능이 좋다.
하지만 여전히 Gradient Descent의 속도 저하가 일어난다.
3) ReLU function
가장 많이 쓰이는 함수.
무슨 함수를 써야 할지 모르면 이걸 쓰는 것이 좋다.
sigmoid, tanh의 vanishing gradient 문제를 해결했다.
그래도 아직 절반이 gradient가 0이다.(dying ReLU 현상)
4) Leaky ReLU function
dying ReLU 현상을 해결. (GAN과 같은 train이 어려운 경우에 사용한다.)
하지만 ReLU 보다는 비선형이 덜하다.
지금까지는 어떤 함수가 더 인기 있는지를 알아봤지만 각 구현의 특징에 따라 뭐가 제일 좋을지는 예측하기 힘들다.
어떤 함수가 좋을지 모르겠다면 모두 시도해 본 뒤, 나중에 다룰 검증이나 개발 세트에 시도해보고 결과를 살펴보아야 한다.
그리고 제일 좋은 결과가 나온 걸 선택하면 된다.
여러 선택지를 시도해본다면 나의 NN에 무엇이 잘 맞는지 알게 될 것이다.
항상 ReLU 함수를 쓴다고 했지만, 나중에 풀어야 하는 문제에 적용되지 않을 수도 있다.
Non-linear activation functions
NN가 함수를 계산하려면 non-linear activation function이 필요하다.
다음은 위에서 본 식이다.
$z^{[1]}=W^{[1]}a^{[0]}+b^{[1]}$
$a^{[1]}=g(z^{[1]})$
$z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}$
$a^{[2]}=g(z^{[2]})$
여기서 함수 g를 없애고 $z^{[1]}$로 대체해보자.
즉, $g(z)=z$인 것이다.
이걸 linear activation function이라고 부른다.
$z^{[1]}=W^{[1]}a^{[0]}+b^{[1]}$
$a^{[1]}=z^{[1]}$
$z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}$
$a^{[2]}=z^{[2]}$
위의 식을 이렇게 바꾼다면 이 모델은 $\hat{y}$을 x에 대한 linear function으로 계산하게 된다.
이 식은 또한 다음과 같이 나타낼 수 있다.
$a^{[1]}= z^{[1]}= W^{[1]}a^{[0]}+b^{[1]}$
$a^{[2]}= z^{[2]}= W^{[2]}a^{[1]}+b^{[2]}$
그리고 $a^{[1]}$을 두 번째 식에 대입한다면,
$a^{[2]}= W^{[2]}(W^{[1]}a^{[0]}+b^{[1]})+b^{[2]}$
이 식이 나온다.
마지막으로 이 식을 간소화하면
$a^{[2]}= (W^{[2]}W^{[1]})x+(W^{[2]}b^{[1]}+b^{[2]})$가 된다.
이처럼 linear activation function만 쓴다면 NN은 입력의 linear function만을 출력하게 된다.
나중에 layer가 많은 NN인 deep network에 대해 다룰 텐데, layer가 얼마나 많든 간에 NN은 linear activation function만 계산하기 때문에 hidden layer가 없는 것과 다름없다.
즉, 여기서 알아야 할 점은 linear hidden layer는 쓸모가 없다는 것이다.
두 linear function의 조합은 하나의 linear function이 되기 때문이다.
non-linear function을 쓰지 않는다면 NN이 깊어져도 흥미로운 계산을 할 수 없다.
linear activation function인 $g(z)=z$를 쓸 데가 하나 있는데 regression 문제에 대한 머신러닝을 할 때이다.
즉, 집 값을 예측할 때 같은 경우인 y가 실수일 때이다.
y가 0이나 1이 아닌 0부터 집값이 비싸지는 대로 올라간다.
이처럼 y가 실수 값이라면 linear activation 함수를 써도 괜찮다.
출력 값인 $\hat{y}$이 -∞부터 +∞까지의 실수 값이 되도록 말이다.
하지만 hidden unit은 linear activation function이 아닌 다른 non-linear activation function을 써야 한다.
linear activation function을 쓸 수 있는 곳은 대부분 output layer이다.
Derivatives of activation functions
1) sigmoid activation function
$g(z)=a=\frac{1}{1+e^{-z}}$
$g^\prime(z)={d \over dz}g(z)=\frac{1}{1+e^{-z}}=g^{(z)}(1-g(z))$
$g^\prime(z)=a(1-a)$
2) tanh activation function
$g(z)=a=tanh(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}$
$g^\prime(z)={d \over dz}g(z)=1-(tanh(z))^2$
$g^\prime(z)=1-a^2$
3) ReLU and Leaky ReLU
ReLU
$g(z)=max(0,z)$
$g^\prime(z)=\begin{cases} 0 & \mbox{if }z\mbox{<0} \\ 1 & \mbox{if }z\mbox{>=0} \end{cases}$
Leaky ReLU
$g(z)=max(0.01z,z)$
$g^\prime(z)=\begin{cases} 0.01 & \mbox{if }z\mbox{<0} \\ 1 & \mbox{if }z\mbox{>=0} \end{cases}$
Random Initialization
NN을 training 할 때 변수를 임의 값으로 초기화하는 것은 중요하다.
logistic regression의 경우 모두 0으로 초기화해도 괜찮지만, NN에서 모두 0으로 초기화하고 Gradient Descent를 적용할 경우 올바르게 동작하지 않는다.
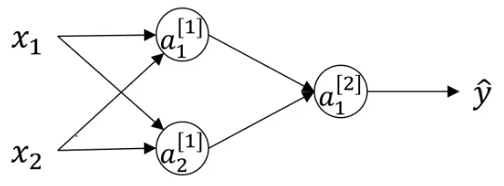
여기에서는 두 개의 input unit을 가진다. → $n^{[0]}=2$
그리고 두 개의 hidden unit을 가진다. → $n^{[1]}=2$
다음 그림처럼 hidden layer에 관한 행렬은 $W^{[1]}=(2, 2)$이고 모두 0으로 초기화한다.
$W^{[1]}=\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}$
$b^{[1]}$ 또한 0으로 초기화한다.
$b^{[1]}=\begin{bmatrix} 0 \\ 0 \end{bmatrix}$
b를 0으로 초기화하는 것은 실제로는 괜찮다.
하지만 W까지 모두 0으로 초기화하는 것은 문제가 될 수 있다.
여기서 발생하는 문제는 어떤 sample의 경우에도 $a^{[1]}_1$과 $a^{[1]}_2$가 같은 값을 가진다는 것이다.
두 hidden unit 모두 정확히 같은 함수를 계산하기 때문이다.
또한 $dz^{[1]}_1$과 $dz^{[1]}_2$ 도 같은 결과를 가지게 된다는 것을 알 수 있다.
그리고 $W^{[2]}=\begin{bmatrix} 0 & 0 \end{bmatrix}$가 될 것이다.
$W^{[1]}=\begin{bmatrix} u & u \\ u & u \end{bmatrix}$
이 NN을 이렇게 초기화하는 경우에 $a^{[1]}_1$ unit과 $a^{[1]}_2$ unit은 완전히 같은 것이 된다.
따라서 이것을 'completelt symmetric(완전 대칭)'이라고 말할 수 있다.
완전히 같은 함수를 계산한다는 것이다.
수학적 귀납법을 사용하면 각 훈련의 반복마다 두 hidden unit은 항상 같은 함수를 계산한다는 것을 알 수 있다.
NN이 얼마나 많은 training을 하는지에 상관없이 두 hidden unit은 항상 같은 함수를 가지는 것이다.
따라서 이 경우에 hidden unit이 항상 같은 것을 계산하기 때문에 실제로 한 개라고 할 수 있다.
또한 더 큰 규모를 가지는 NN의 경우를 보면, 세 개의 input unit이 있고 매우 많은 hidden unit이 있는 경우에도 비슷한 논리가 적용된다.
모든 값을 0으로 초기화한다면 모든 hidden unit은 대칭이 되고 Gradient Descent를 얼마나 적용시키는지에 상관 없이 모든 unit은 항상 같은 함수를 계산하게 될 것이다.
따라서 이것은 쓸모없게 된다.
다른 함수를 계산하기 위한 각각 다른 unit이 필요하기 때문이다.
이것의 해결 방법은 변수를 임의로 초기화하는 것이다.
$W^{[1]}=np.random.randn((2,2))$을 사용한다.
np.random.randn 함수는 가우시안 랜덤 변수를 생성한다.
그렇게 되면 일반적으로 이 값에 0.01과 같은 굉장히 작은 수를 곱해준다. → $W^{[1]}=np.random.randn((2,2))*0.01$
※0.01과 같은 굉장히 작은 수를 곱해주는 이유는,
$z^{[1]}=W^{[1]}x+b^{[1]}$
$a^{[1]}=g^{[1]}(z^{[1]})$이다.
이때 W가 큰 값을 가지는 경우에 z도 굉장히 큰 값을 가지거나 몇몇 값이 굉장히 크거나 작은 상태가 될 수 있다.
tanh function이나 sigmoid function에서 z값이 굉장히 크거나 작은 값을 가지는 경우, 경사의 기울기가 매우 낮기 때문에 Gradient Descent 또한 매우 느리게 적용된다.
따라서 학습 속도가 느려지게 된다.
결론적으로 W가 너무 큰 값을 가지면 매우 큰 값의 z를 이용해 training을 시작하게 되고 tanh activation function이나 sigmoid activation function이 너무 큰 값을 가지게 되므로 학습의 속도가 느려진다.
따라서 0.01과 같은 작은 수를 곱해주는 것이고 이외에 다른 작은 수를 곱해도 괜찮다.
따라서 굉장히 작은 임의의 수를 초기값으로 만들어낼 수 있다.
$b^{[1]}$의 경우 방금과 같은 대칭 문제를 가지지 않는다.
이 문제를 대칭 회피 문제라고 부른다.
따라서 $b^{[1]}$을 0으로 초기화하는 것은 괜찮기 때문에
$b^{[1]}=np.zeros((2,1))$을 사용한다.
비슷한 방법으로 $W^{[2]}$도 임의의 값으로 초기화할 수 있다. → $W^{[2]}=np.random.randn((1,2))*0.01$
$b^{[2]}$도 마찬가지로 0으로 초기화하면 된다.
적은 hidden layer를 가진 상대적으로 얕은 NN에서는 0.01을 곱하는 것도 괜찮지만, 매우 깊은 깊이의 NN을 training 하는 경우에는 0.01과는 다른 수를 선택할 수도 있을 것이다.
'Computer Science > Deep Learning' 카테고리의 다른 글
| 미래연구소 딥러닝 5주 차 (0) | 2020.08.09 |
|---|---|
| 미래연구소 딥러닝 4주 차 (Numpy 특강 3) (0) | 2020.08.02 |
| 미래연구소 딥러닝 3주 차 ( Numpy 특강 2) (0) | 2020.07.25 |
| 미래연구소 딥러닝 3주 차 (0) | 2020.07.25 |
| 미래연구소 딥러닝 2주 차 (0) | 2020.07.19 |
