미래연구소 http://futurelab.creatorlink.net/
미래연구소
AI, 인공지능 Deep Learning beginner 미래연구소 딥러닝 입문 스터디 / 모집인원 : 25명 (선착순 마감) 수강료 : 월 15만원 / (Coursera 강의 수강료 월 5만원 개인결제)
futurelab.creatorlink.net
C1W4L01 Deep L-layer Neural network
What is a deep neural network?
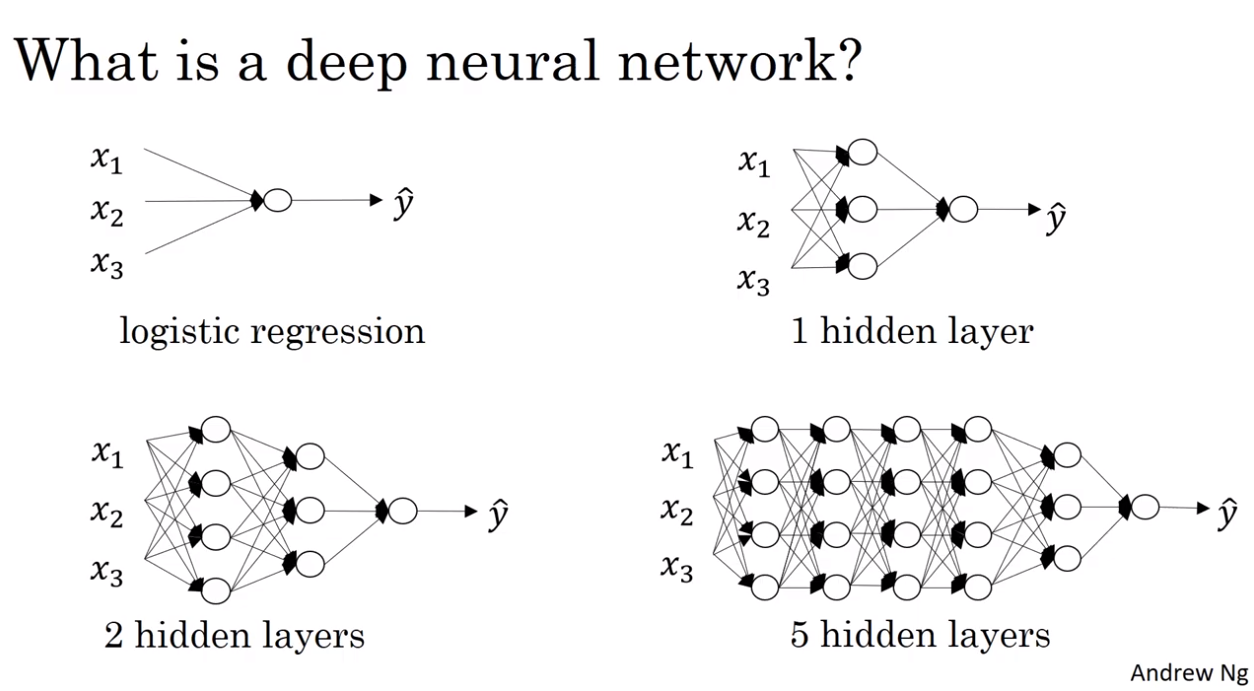
Logistic regression은 매우 얕은 모델이라고 한다.
반면에 5 hidden layer를 가진 “6 layer” NN은 더 깊은 모델이다.
1 hidden layer를 가진 “2 layer” NN은 여전히 얕지만 logistic regression만큼은 아니다.
지난 몇 년 동안 Machine Learning이 얕은 모델은 보통 할 수 없는 학습을 Deep Neural Network(DNN)로 가능하게 하는 함수가 있다는 것을 깨달았다.
비록 주어진 어떤 문제에 대해서 얼마나 깊은 NN을 사용해야 하는지 미리 정확하게 예측하기는 어려울 것이다.
따라서 logistic regression을 시도하고 그다음에 2 hidden layers를 시도한다.
개발 설정 과정에서 다양한 값을 시도하고 검증 데이터에서 평가한다.
Deep neural network notation

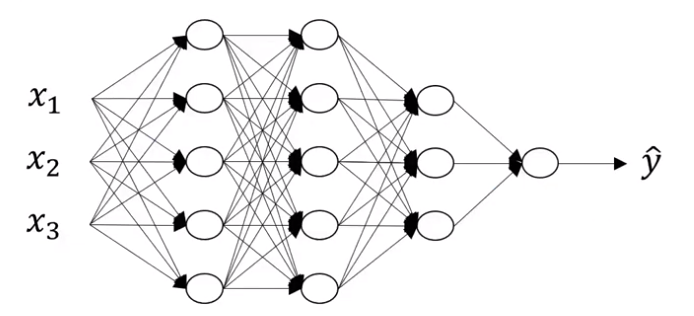
L은 layer의 개수를 표시한다.
→L=4
$n^{[l]}$은 layer l의 unit의 개수이다.
→$n^{[0]}=n_x=3, n^{[1]}=5, n^{[2]}=5, n^{[3]}=3, n^{[4]}=n^{[L]}=1$
$a^{[l]}$은 layer l에서의 activation을 나타낸다.
→$a^{[l]}=g^{[l]}(z^{[l]})$
$w^{[l]}, b^{[l]}$도 $z^{[l]}$의 값을 계산하기 위한 가중치를 나타내기 위해 사용된다.
Input은 X라고 부르며, X는 층 0의 activation과 같다.
따라서 $a^{[0]}=X$이다.
마지막 layer의 activation인 $a^{[L]}$은 $\hat{y}$과 같다.
C1W4L02 Forward propagation in a deep network
Forward propagation in a deep network
$z^{[1]}=w^{[1]}a^{[0]}+b^{[1]}$
$a^{[1]}=g^{[1]}(z^{[1]})$
$z^{[2]}=w^{[2]}a^{[1]}+b^{[2]}$
$a^{[2]}=g^{[2]}(z^{[2]})$
$z^{[3]}=w^{[3]}a^{[2]}+b^{[3]}$
$a^{[3]}=g^{[3]}(z^{[3]})$
$z^{[4]}=w^{[4]}a^{[3]}+b^{[4]}$
$a^{[4]}=g^{[4]}(z^{[4]})$
이 식들로 알 수 있는 일반적인 forward propagation의 수식은
$z^{[l]}=w^{[l]}a^{[l-1]}+b^{[l]}$
$a^{[l]}=g^{[l]}(z^{[l]})$
이다.
전체 training set에 대한 vectorization은 다음과 같다.
$Z^{[1]}=w^{[1]}A^{[0]}+b^{[1]}$
$A^{[1]}=g^{[1]}(Z^{[1]})$
$Z^{[2]}=w^{[2]}A^{[1]}+b^{[2]}$
$A^{[2]}=g^{[2]}(Z^{[2]})$
$Z^{[3]}=w^{[3]}A^{[2]}+b^{[3]}$
$A^{[3]}=g^{[3]}(Z^{[3]})$
$Z^{[4]}=w^{[4]}A^{[3]}+b^{[4]}$
$A^{[4]}=g^{[4]}(Z^{[4]})$
$(Z^{[l]}=\begin{bmatrix} z^{[l](1)} & z^{[l](2)} \cdots & z^{[l](m)} \end{bmatrix})$
이를 통해 위에서 정리했던 일반적인 수식을 수정하면
$Z^{[l]}=w^{[l]}A^{[l-1]}+b^{[l]}$
$A^{[l]}=g^{[l]}(Z^{[l]})$
이다.
위의 수식을 반복문(for l=1…4)을 사용하여 각각의 layer에 대해 activation을 계산해야 한다.
Network를 구현할 때 보통 명시적인 반복문은 피하고 싶어 한다.
그러나 명시적인 반복문 외에 이 부분을 구현할 수 있는 다른 방법이 없다고 한다.
따라서 forward propagation을 구현할 때 각 layer에 대한 activation을 계산하는 반복문을 사용하는 것은 괜찮다.
C1W4L03 Getting your matrix dimensions right
Parameters $W^{[l]}$ and $b^{[l]}$

다음 그림에서 $n^{[0]}=n_x=2, n^{[1]}=3, n^{[2]}=5, n^{[3]}=4, n^{[4]}=2, n^{[5]}=1$인 것을 알 수 있다.
그리고 $z^{[1]}=W^{[1]}a^{[0]}+b^{[1]}$일 때,
$a^{[0]}$은 (2,1)인 것과 $z^{[1]}$은 (3,1)인 것을 알 수 있다.
(3, 1)=(?, ?)(2, 1)이므로 $W^{[1]}$은 (3,2)인 것 또한 알 수 있다.
이는 $(n^{[1]}, n^{[0]})$이다.
이와 같은 방법으로 다른 $W^{[l]}$을 구해본다면,
Layer l에 대한 행렬의 일반적인 수식을 보면 $W^{[l]}: (n^{[l]}, n^{[l-1]})$이다.
$b^{[l]}$은 $z^{[l]}$이 $(n^{[l]}, 1)$이 되기 위해서,
Layer l에 대한 행렬의 일반적인 수식은 $b^{[l]}: (n^{[l]}, 1)$이다.
$W^{[l]}: (n^{[l]}, n^{[l-1]})$
$b^{[l]}: (n^{[l]}, 1)$
이 두 수식을 이용해 W와 b vector가 올바른 차원을 가지는지 확인해볼 수 있다.
추가로 $dW^{[l]}$의 차원은 $W^{[l]}$의 차원과 같아야 한다.
또한 $db^{[l]}$의 차원은 $b^{[l]}$의 차원과 같아야 한다.
Vectorized implementation
Vectorization인 $Z^{[l]}$은
$(Z^{[l]}=\begin{bmatrix} z^{[l](1)} & z^{[l](2)} \cdots & z^{[l](m)} \end{bmatrix})$
이므로 $(n^{[l]}, m)$이다.
마찬가지로 $A^{[l]}$은 $(n^{[l]}, m)$이다.
$b^{[l]}$은 여전히 $(n^{[l]}, 1)$이다.
하지만 $b^{[l]}$은 파이썬 broadcasting을 통해 $(n^{[l]}, m)$ 행렬이 된다.
위의 내용들을 정리하면 다음과 같다.
$z^{[l]}, a^{[l]}: (n^{[l]}, 1)$
$dz^{[l]}, da^{[l]}: (n^{[l]}, 1)$
$Z^{[l]}, A^{[l]}: (n^{[l]}, m)$
$dZ^{[l]}, dA^{[l]}: (n^{[l]}, m)$
C1W4L04 Why deep representations?
Intuition about deep representation
여러 개의 hidden layer를 갖는 DNN은 낮은 단계에서는 간단한 특징을 학습하게 되고, 그 후 깊은 층에서는 탐지된 간단한 것들을 함께 모아 더 복잡한 것들을 탐지하게 된다.
초기의 층에서 계산되는 것은 상대적으로 간단한 함수로 보인다.
Network가 더 깊어질수록 놀라울 만큼 복잡한 것들(얼굴 인식, 단어, 구, 문장 인식)이 가능해진다.
Circuit theory and deep learning
상대적으로 작지만 깊은 DNN에서 계산할 수 있는 함수가 있다.
작다는 것은 hidden layer의 개수가 상대적으로 작다는 것을 의미한다.
그러나 얕은 Network로 같은 함수를 계산하려고 하면 즉, 충분한 hidden layer가 없다면
기하급수적으로 많은 hidden unit이 계산에 필요하게 될 것이다.
가끔 처음부터 너무 많은 hidden layer를 사용하려고 할 때가 있다.
그러나 새로운 문제를 직면하면 logistic regression부터 시작해서 1 hidden layer 혹은 2 hidden layer를 시도하는 것이 좋다.
그러나 지난 몇 년 간 일부 애플리케이션에서 아주 깊은 NN을 만드는 경향이 있었다.
어떤 문제에 관해서는 이것이 최고의 모델이 될 수도 있다.
C1W4L05 Building blocks of deep neural networks
Forward and backward functions

Layer l에서 forward function과 backward function이 있다.
Forward function에서 input으로 $a^{[l-1]}$이 들어가면, output으로 $a^{[l]}$이 나온다.
계산을 위해서 $W^{[l]}, b^{[l]}$을 사용해야 한다.
또한 $z^{[l]}$이 포함된 cache도 출력된다.
Backward function은 또 다른 function이 된다.
Input으로 $da^{[l]}$을 넣으면, output으로 $da^{[l-1]}$이 나온다.
이때도 계산을 위해서 $W^{[l]}, b^{[l]}$을 사용하고,
계산 과정에 따라 $dz^{[l]}$도 얻는다.
이 backward function은 $dW^{[l]}, db^{[l]}$를 출력한다.
C1W4L06 Forward and backward propagation
Forward propagation for layer l
$Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]}$
$A^{[l]}=g^{[l]}(Z^{[l]})$
Backward propagation for layer l
$dz^{[l]}=dA^{[l]}g^{\prime[l]}(Z^{[l]})$
$dW^{[l]}=\frac{1}{m}dZ^{[l]}A^{[l-1]T}$
$db^{[l]}=\frac{1}{m}np.sum(dZ^{[l]}, axis=1, keepdims=True)$
$dA^{[l-1]}=W^{[l]T}dZ^{[l]}$
Summary

C1W4L07 Parameters vs Hyperparameters
What are hyperparameters?
Hyperparameter에는 다음과 같은 것들이 있다.
-
Learning rate $\alpha$
-
iterations(Gradient Descent의 반복 횟수)
-
hidden layer L
-
hidden units $n^{[1]}, n^{[2]}, \cdots$
-
choice of activation functions (ReLU, tanh, sigmoid)
이 모든 것들을 learning algorithm에 알려줘야 한다.
이 매개변수들은 궁극적으로 매개변수 W와 b를 통제한다.
따라서 이 매개변수들을 hyperparameter라고 부른다.
이렇게 많은 hyperparameter가 없었던 machine learning 초기 시대에는 대부분의 사람들이 learning rate($\alpha$)를 parameter라고 불렀다.
기술적으로 $\alpha$는 parameter가 맞긴 하지만, 정확히는 진짜 parameter를 결정하는 parameter이다.
따라서 $\alpha$, interations 등을 hyperparameter라고 부른다.
Applied deep learning is a very empirical process
$\alpha$의 값을 정하는 방법은 우선 값을 설정하는 시도를 여러 번 한 뒤, 어떤 $\alpha$값이 학습을 꽤 빠르게 하고 더 낮은
cost function J로 수렴한다면 이 $\alpha$값을 사용하게 된다.
앞에서 본 것처럼 다양한 hyperparameter가 있다.
새로운 애플리케이션을 시작할 때 hyperparameter의 가장 적합한 값을 정확히 미리 아는 것은 매우 어렵다.
따라서 자주 사용하는 방법은, 다양한 값을 시도하고 아래 그림의 사이클을 따라서 몇 가지 값들을 시도하는 것이다.

또한 이런 몇 가지 값들로 시도를 해볼 때, hyperparameter의 조건을 하나씩만 바꿔서 시도해보는 것이 좋다.
이 장의 제목은 ‘딥러닝을 적용하는 것은 매우 경험적인 과정이다.’이다.
경험적인 과정이라는 것은 많은 것을 시도하고 작동되는지를 확인한다는 것이다.
C2W1L01 Train / dev / test sets
Applied ML is a highly iterative process
NN을 training 시킬 때는 많은 결정을 내려야 한다.
NN이 몇 개의 layer를 가지는지,
각각의 layer가 몇 개의 hidden unit을 가지는지,
Learning rate는 무엇인지,
서로 다른 layer에서 사용하는 activation function은 무엇인지 …
새로운 애플리케이션을 시작할 때는 이 모든 것에 대한 올바른 값을 추측하는 것이 거의 불가능하다.
(David Wolpert: The supervised learning no-free-lunch theorems. → 아무거나 선택한 hyperparameter가 free lunch 일리가 없고 여러 번 시도해야 lunch를 얻을 수 있다는 의미. 즉, data set마다 최적의 hyperparameter가 다 달라서 여러 번 시도해서 최적의 hyperparameter를 찾아내야 한다.)
다른 hyperparameter에 대해서도 마찬가지이다.
따라서 실질적으로 ML을 적용하는 것은 매우 반복적인 과정(iterative process)이다.이다.
즉, 오늘날 DL을 적용하는 것은 애플리케이션의 네트워크에 대한 좋은 선택을 찾기 위해 이 사이클(사진 5-4 참고)을 여러 번 돌아야 하는 매우 반복적인 과정이다.
따라서 빠른 진전을 이루는데 영향을 미치는 것들은 이 사이클을 얼마나 효율적으로 돌 수 있는지와 데이터 세트를 잘 설정하는 것이다.
Train / dev / test sets
train, develop, test sets를 잘 설정하는 것은 과정을 더 효율적으로 만든다.
전통적인 방법은 모든 데이터를 가져와서 일부는 train set, 일부는 dev set, 나머지는 test set으로 만든다.
작업의 흐름은 train set에 대해 계속 training algorithm을 적용시키면서 dev set에 대해 다양한 모델 중 어떤 모델이 가장 좋은 성능을 내는지 확인한다.
(dev set은 hold-out set이라고도 한다. holdout set이라는 용어는 data를 다 쓰지 않고 검증을 위해 남겨둔다는 의미를 담고 있다.)
총 100개, 1000개, 10000개의 sample의 경우에 60:20:20 비율은 경험에서 나온 가장 합당한 비율이었다.
그러나 총 100만 개 이상의 sample이 있는 현대 빅데이터 시대에는 dev set와 test set이 훨씬 더 작은 비율이 되는 것이 트렌드가 되었다.
왜냐하면 dev set와 test set의 목표는 서로 다른 알고리즘을 시험하고 어떤 알고리즘이 더 잘 작동하는지 확인하는 것이기 때문에 dev set은 평가할 수 있을 정도로만 크면 된다.
이를 위해 전체 데이터의 20%나 필요하지는 않다.
따라서 예를 들어 100만 개의 sample이 있는 경우에는 10000개 정도의 dev set만으로도 두 개의 알고리즘 중 어느 것이 더 좋은지 평가하는데 충분하다.
같은 방식으로 test set의 주요 목표는 최종 알고리즘이 어느 정도 성능인지 신뢰 있는 추정치를 제공하는 것이므로 100만 개의 sample이 있을 때 10000개 정도의 sample을 설정해도 충분하다.
결과적으로 빅데이터에서는 98:1:1 비율을 가진다.
100만 개보다 많은 sample을 가지는 애플리케이션의 경우에는 dev set와 test set의 비율이 더 낮을 수도 있다.
Mismatched train/test distribution
현대 DL의 또 다른 트렌드는 더 많은 사람들이 일치하지 않는 train/test 분포에서 training 시키는 것이다.
만약 training set은 전문가스럽고 잘 정돈된 고양이 사진이고, dev/test set은 흐릿한 저해상도의 고양이 사진이라면 이 두 가지 데이터의 분포는 달라질 수 있다.
이런 경우에는 dev set과 test set가 같은 분포에서 와야 머신러닝 알고리즘의 진전은 더 빠르게 일어난다.
C2W1L02 Bias/Variance
Bias/Variance
Train set error가 1% 일 때 Dev set error가 11%인 경우에는, train set에서는 분류가 매우 잘 됐지만 상대적으로 dev set에서는 잘 분류되지 못했다.
즉, train set에서 over fit 되어, dev set이 있는 교차 검증 세트에서 (cross validation service) 일반화되지 못한 경우이다.
(fit이란 train과 동의어, 너무 잘 맞을 때=over fit, 너무 안 맞을 때=under fit
overfit일 경우 모델이 너무 복잡해질 수 있다.
모델이 복잡해지면 학습하지 않은 데이터들에 대해서는 성능이 안 좋다.)
이런 경우에는 높은 분산(high variance)을 갖는다고 말한다.
따라서 train set error와 dev set error를 살펴봄으로써 알고리즘이 높은 분산을 갖는다는 것을 진단할 수 있게 된다.
이번에는 train set error가 15%이고 dev set error가 16%인 경우가 있다.
이 경우에 인간은 대략 0%의 오차를 낸다고 가정한다.
그럼 이 알고리즘은 train set에 대해서도 잘 작동되지 않는 것처럼 보인다.
Train set에 대해서도 잘 맞지 않는다면 데이터에 과소 적합(under fit)한 것이다.
이런 경우에는 높은 편향(high bias)를 갖는다고 말한다.
또 다른 경우에 train set error는 15%, dev set error는 30%이다.
이 경우에는 train set error가 너무 높은 비율을 가지고 있으므로 알고리즘이 high bias를 갖는다고 진단 내릴 것이다.
또한 high variance도 가지고 있다.
이 경우도 under fit 하다.
마지막 경우는 train set error는 0.5%이고 dev set error는 1%이다.
사용자는 1%의 오차만 있는 이 알고리즘에 만족할 것이다.
이 경우에는 low bias와 low variance를 가지고 있기 때문이다.
'Computer Science > Deep Learning' 카테고리의 다른 글
| 미래연구소 딥러닝 6주 차 (0) | 2020.08.16 |
|---|---|
| 미래연구소 딥러닝 4주 차 (Numpy 특강 3) (0) | 2020.08.02 |
| 미래연구소 딥러닝 4주 차 (0) | 2020.08.02 |
| 미래연구소 딥러닝 3주 차 ( Numpy 특강 2) (0) | 2020.07.25 |
| 미래연구소 딥러닝 3주 차 (0) | 2020.07.25 |
